Ahmed Bou-Rabee


Courant Institute
Department of Mathematics
Office: 1007 Warren Weaver Hall
Email:   ahmedmb@gmail.com

I am an NSF Postdoctoral Fellow at the Courant Institute sponsored by Scott Armstrong. I began my fellowship at Cornell University sponsored by Lionel Levine. I received my PhD at the University of Chicago under the supervision of Charles K. Smart in June 2022. Previously, I received a B.S. in mathematics and an M.S. in statistics from Stanford University.

I am interested in probability and partial differential equations. Some topics I have worked on include quantitative stochastic homogenization, the Abelian sandpile, and Liouville quantum gravity.

Publications and Preprints

  1. Random walk on sphere packings and Delaunay triangulations in arbitrary dimension, with Ewain Gwynne. [arXiv:2405.11673]
  2. Superdiffusive central limit theorem for a Brownian particle in a critically-correlated incompressible random drift, with Scott Armstrong and Tuomo Kuusi. [arXiv:2404.01115] [Blog]
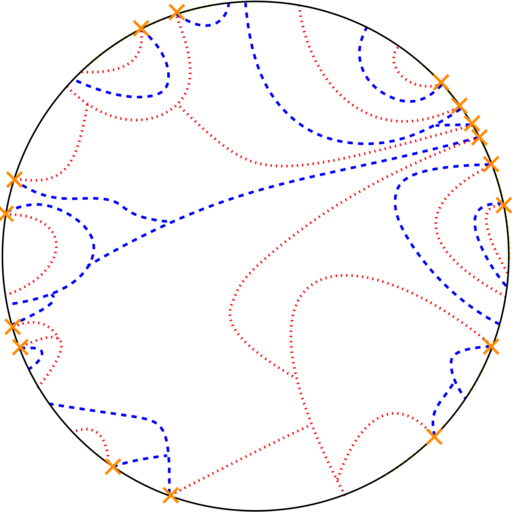
  3. Unique continuation on planar graphs, with Bill Cooperman and Shirshendu Ganguly. [arXiv:2309.13728]
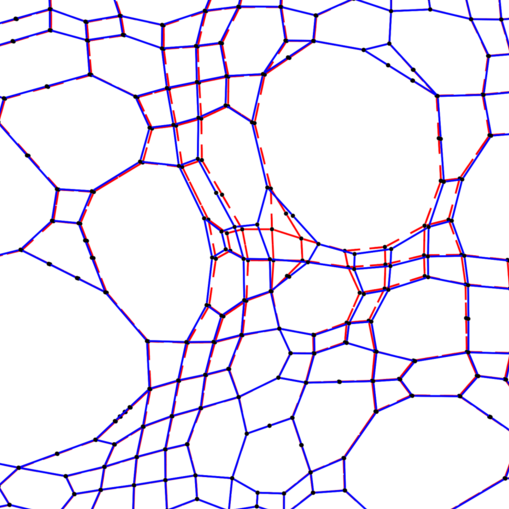
  4. Rigidity of harmonic functions on the supercritical percolation cluster, with Bill Cooperman and Paul Dario. Transactions of the American Mathematical Society, to appear. [arXiv:2303.04736]
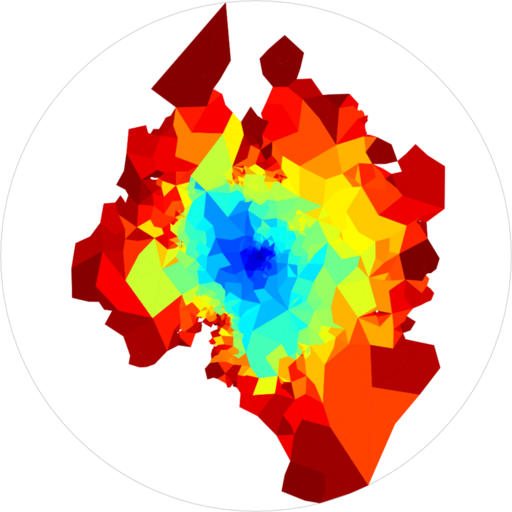
  5. Internal DLA on mated-CRT maps, with Ewain Gwynne. Annals of Probability, to appear. [arXiv:2211.04891]
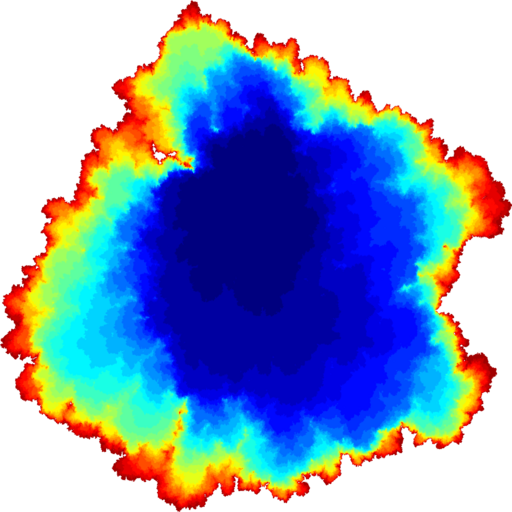
  6. Harmonic balls in Liouville quantum gravity, with Ewain Gwynne. [arXiv:2208.11795]
  7. Integer superharmonic matrices on the F-lattice. Advances in Mathematics, 436, 109400 (2024). [Journal] [arxiv:2110.07556] [Extended Appendix] [Code]
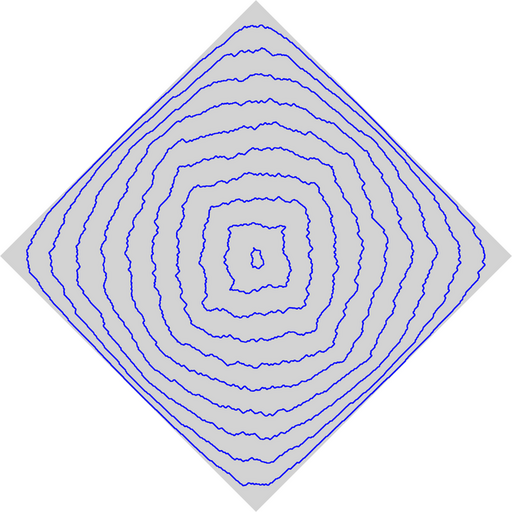
  8. Hamilton-Jacobi scaling limits of Pareto peeling in 2D, with Peter S. Morfe. Probability Theory and Related Fields, 188, 235-307 (2024). [Journal] [arXiv:2110.06016] [Code]
  9. A shape theorem for exploding sandpiles. Annals of Applied Probability 34(1A): 714-742 (2024) [Journal] [arxiv:2102.04422] [Notebook]
  10. Dynamic dimensional reduction in the Abelian sandpile. Communications in Mathematical Physics , 390, 933-958 (2022). [Journal] [arxiv:2009.05968] [Code]
  11. Convergence of the random Abelian sandpile. Annals of Probability 49(6): 3168-3196 (2021). [Journal] [arxiv:1909.07849] [Pictures]

Talks

Coding

Teaching